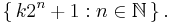Sierpinski number

In number theory, a Sierpinski or Sierpiński number is an odd natural number k such that k2n + 1 is composite, for all natural numbers n; in 1960, Wacław Sierpiński proved that there are infinitely many odd integers k which have this property.

In other words, when k is a Sierpinski number, all members of the following set are composite:

\left\{\,k 2^n %2B 1�: n \in\mathbb{N}\,\right\}.

Numbers in this set with odd k and k < 2n are called Proth numbers.

Contents

Known Sierpinski numbers

The sequence of currently known Sierpinski numbers begins with:

78557, 271129, 271577, 322523, 327739, 482719, 575041, 603713, 903983, 934909, 965431, … (sequence A076336 in OEIS).

The number 78,557 was proved to be a Sierpinski number by John Selfridge in 1962, who showed that all numbers of the form 78557·2n+1 have a factor in the covering set {3, 5, 7, 13, 19, 37, 73}. For another known Sierpinski number, 271129, the covering set is {3, 5, 7, 13, 17, 241}. All currently known Sierpinski numbers possess similar covering sets.[1]

The Sierpinski problem

Main article: Seventeen or Bust
Unsolved problems in mathematics
Is 78,557 the smallest Sierpinski number?

The Sierpinski problem is: "What is the smallest Sierpinski number?"

In 1967, Sierpiński and Selfridge conjectured that 78,557 is the smallest Sierpinski number, and thus the answer to the Sierpinski problem.

To show that 78,557 really is the smallest Sierpinski number, one must show that all the odd numbers smaller than 78,557 are not Sierpinski numbers. That is, for every odd k below 78,557 there exists a positive integer n such that k2n+1 is prime.[1] As of August 2010, there are only six candidates:

k = 10223, 21181, 22699, 24737, 55459, and 67607

which have not been eliminated as possible Sierpinski numbers.[2] Seventeen or Bust (with PrimeGrid), a distributed computing project, is testing these remaining numbers. If the project finds a prime of the form k2n+1 for every remaining k, the Sierpinski problem will be solved.

See also

References

  1. ^ a b Sierpinski number at The Prime Glossary
  2. ^ Seventeen or Bust: Project Stats

Further reading

External links